浮動小数点数の二段階丸め誤差
さいきん『浮動小数点数小話』という同人誌を読んでFMA (Fused Multiply-Add)の二段階丸め誤差(double rounding error)について色々と知る機会があったのでまとめておく。ついでにFMAに関するOpenJDKのバグっぽい挙動を見つけたのでそれも併せて記しておく。
FMA (Fused Multiply-Add)とは
FMAは以下のような演算のことを呼ぶ。
\[fma(x, y, z) = xy + z\]この演算自体は行列の乗算やベクトルの内積の計算でよく現れるものであるが、通常の浮動小数点数の乗算と加算を別々に行うと誤差が出るので一度の演算で正確な値を算出したいときに用いる。たとえばC言語(C99)では fma、fmaf、fmalという3つの関数が導入されているらしい。
FMAの実装における二段階丸め誤差
FMAはターゲットとなるCPUのアーキテクチャがFMA命令をサポートしていればその命令を直接呼び出すことで(バグがなければ)誤差なく求める答えを得ることができる。一方でそうでない場合はソフトウェア的にFMAをエミュレートしてやる必要がある。『浮動小数点数小話』では、高精度の型で演算して低精度の型に変換する実装をよくある実装ミスとして挙げている。
public static float(float x, float y, float z) {
return (float)((double) x * (double) y + (double) z)
}
このコードは一見すると正しそうに見える。むかし授業で習った数値誤差の話でも計算過程で有効桁数の2倍を担保していれば計算で誤差が入らなかったような気がするし、実際、単精度(float)の桁数は24で倍精度(double)の桁数は53なので十分と思うかもしれない。しかし、これは無限精度で計算してfloatに一度だけ丸めたものとは結果が異なってしまう。
以下のコードを実行してみよう。
public class Test {
public static void main(String[] args) {
float x = 0x1.fffffep23f;
float y = 0x1.000004p28f;
float z = 0x1.fep5f;
System.out.printf("%a\n", fma(x, y, z)); // 0x1.000004p52
}
public static float fma(float a, float b, float c) {
return (float)((double) a * (double) b + (double) c);
}
}
出力される結果は 0x1.000004p52 だが、これは本来の結果とは異なる。無限精度で計算すると x * y + z は 0x1.000002fffffffcp52 となり、これをfloatに丸めると 0x1.000002p52 となるはずだ。
この差がどこに由来するか考えると、じつは + (double) c の加算においてdouble型に丸めたときと、そこからさらに (float) でfloat型に丸めたときとで二段階に丸めていることが問題であることがわかる。つまり 0x1.000002fffffffcp52 -(double丸め)→ 0x1.0000030000000p52 -(float丸め)→ 0x1.000004p52 となっている。これを図示するとつぎのようになる。
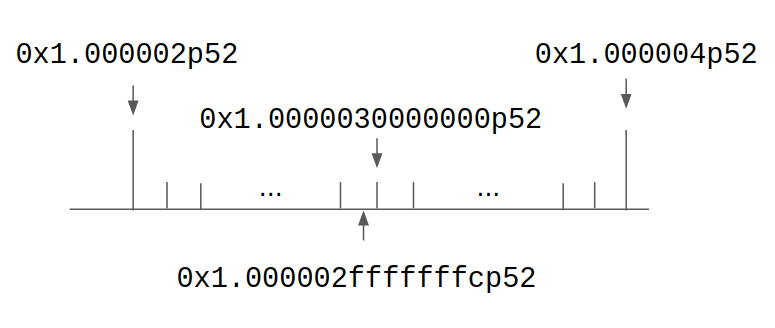
図の数直線上の短い直線はdoubleで表せる実数を、長い直線はfloatで表せる実数を示している。無限精度での答え 0x1.000002fffffffcp52 はfloatの観点からは 0x1.000002p52 により近いが、doubleに丸めるときに 0x1.0000030000000p52 になり、さらにfloatに丸めるときは最近接偶数丸めにより 0x1.000004p52 になってしまう。なお、floatの仮数部は23桁なので 0x1.000002p52 の仮数部の最下位1ビットは 1 となることに注意。
OpenJDKのFMA実装のバグ
ついでなので、Java 9から追加された Math.fma(float, float, float) でどうなるかやってみる。
public class Test {
public static void main(String[] args) {
float x = 0x1.fffffep23f;
float y = 0x1.000004p28f;
float z = 0x1.fep5f;
System.out.printf("%a\n", Math.fma(x, y, z)); // 0x1.000002p52
}
}
こんどは 0x1.000002p52 と期待する結果が出力された。めでたしめでたし、となりたいところだが、じつはこの結果は環境依存である。もし使っているCPUアーキテクチャがFMA命令を実装していない場合は、おそらく現時点でのOpenJDKベースのJava(たとえばOracle Java 11.0.8)では 0x1.000004p52 と出力されるはずだ。試みにVM引数で -XX:-UseFMA と付けてみよう。おそらく 0x1.000004p52 という不正確な結果が出力される。
これはOpenJDKの現時点での実装が上で指摘されていたようにdouble型で計算してfloatに戻すという実装になっている(GitHubの該当個所)ためである。
Since the double format moreover has more than (2p + 2) precision bits compared to the p bits of the float format, the two roundings of (a * b + c), first to the double format and then secondarily to the float format, are equivalent to rounding the intermediate result directly to the float format.
コメントにはこのように書いてあるが、この (2p + 2) だから大丈夫という前提が間違っているように思える。OpenJDKには問題を報告しておいた(https://bugs.openjdk.java.net/browse/JDK-8253409)が、priorityも低いのですぐには直らないかもしれない(2021-03-22 追記:修正されたらしい。バックポートもされたらしいので最新版では直っているはず。ちなみに修正方法はBigDecimalを使うというもので面白みはないけれど、そうだろうなという感じでした)。
奇数丸めをつかった実装
さて、二段階丸め誤差を出さないFMAのソフトウェア実装はどうすればよいだろうか。前出の『浮動小数点数小話』によれば “Emulation of a FMA and Correctly Rounded Sums: Proved Algorithms Using Rounding to Odd” という論文に奇数丸めを利用した方法が紹介されているらしい。
これは中間計算を行う際に奇数丸めを常にして最終的な解は通常の最近接偶数丸めをすることで二段階丸め誤差をなくすという話である。実際にさきほどの例で考えると、無限精度での答え 0x1.000002fffffffcp52 をdoubleへ奇数丸めすると 0x1.000002fffffffp52 となるので、そこからfloatへ最近接偶数丸めをすれば 0x1.000002p52 となる。
これがうまくいくのは不思議だが、直観的には最近接偶数丸めで偶数側に寄りがちなのを奇数丸めでバランスを取るということだろう。あるいは、こうも考えることができる。奇数丸めをするということは、doubleの0x1.000002fffffffp52が表す範囲は [0x1.000002fffffffp52, 0x1.0000030000000p52) である。これによって本来の値が 0x1.0000030000000p52 より左ならfloatの 0x1.000002p52 に、右ならfloatの 0x1.000004p52 に丸められるので、最後に最近接偶数丸めをするときに 0x1.0000030000000p52 を飛び越すことがない。
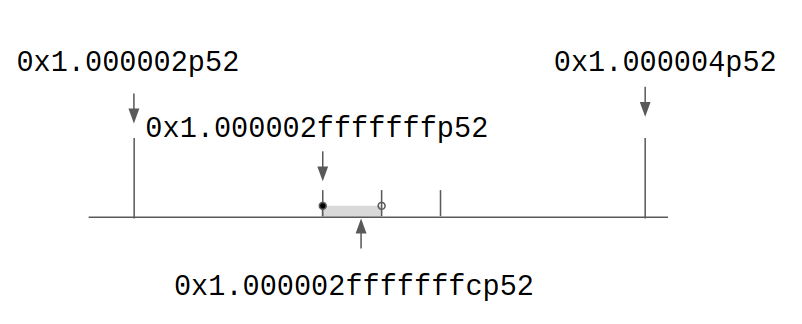
さて、奇数丸めをどう実装するかだが、論文によればDekkerのエラーなし加算器(error-free adder)を使うことでソフトウェア的に奇数丸めを実装できる1。これはつぎのようなアルゴリズムで \({a + b}\) の結果floatに丸めたものを \({s}\) に格納しつつ、本当の値との誤差を \({r}\) で計算できる。そうするとオーバーフローやアンダーフローが発生しなければ \({a + b}\) と \({s + r}\) が厳密に一致することになる。
float s = a + b;
float z = s - a;
float r = b - z;
// a + b = s + r
あとは s の仮数部の偶奇と r の符号を見て奇数丸めを行えばよい。コードにするとこんな感じだろうか。
public static float oddRoundedAdd(float a, float b) {
float s = a + b;
float z = s - a;
float r = b - z;
int sx = Float.floatToIntBits(s);
if ((sx & 1) == 0 && r != 0.0) {
s = Float.intBitsToFloat(sx + (s < 0.0 ^ r > 0.0 ? 1 : -1));
}
return s;
}
以上をまとめて、論文に書かれているFMAのソフトウェア実装をJavaで書くとつぎのようになる。なおfloatのエラーなし乗算はdoubleを使って手を抜いている。
public static float fma(float a, float b, float c) {
float uh = (float) ((double) a * (double) b);
float ul = (float) ((double) a * (double) b - uh);
float th = c + uh;
float tl = uh - (th - c);
return th + oddRoundedAdd(tl, ul);
}
ここで th と tl は c と uh のエラーなし加算の結果である。上記の実装で先ほどの例を実行すると正しく0x1.000002p52が出力されるので、たぶん合っているだろう。なお実際に実装する場合はオーバーフローやアンダーフローも気にする必要があるので、double版のFMAのようにBigDecimalでやってしまう方がらくかもしれない。
ところで、この実装のテストケースを作るのはすごく大変そうだ。floatだとちょうど結果が0.5ULPだけ離れたあたりになるようにサンプルをつくるのが面倒なのだ。doubleなら \({a = 1-2^{-27}, b = 1+2^{=27}, c = 2^{-150}}\)とでもすれば簡単につくれるのだけれど、floatは仮数部の桁数が奇数なのですこしめんどうくさい。
感想
浮動小数点はやはりおもしろい。やはり人間の直感とかなりずれるあたりがおもしろさだろう。floatの四則演算はdoubleを中間表現に使えば誤差なく計算できる、というのは定説であるし、実際に証明もされているが、FMAのような複数の四則演算の組み合わせになると成り立たない、というのは一見不思議にみえる。誤差のない演算を何回繰り返しても誤差が積もらない気がするからだ。しかし、よく考えるとfloat同士の演算をした結果はfloatで表せるとは限らず、さらにその数とfloatとの演算は、すでにfloat同士の四則演算の範囲を出ていると考えれば、「float同士の四則演算は」という部分が成り立たないので、これは矛盾しないわけだ。一方で、doubleは最終的な結果を出すのに十分な表現力を有しているので、途中の演算では奇数丸めを採用するというただそれだけで結果が保証されるというのもおもしろい。Dekker-Knuthのエラーなし加算器も不勉強にして知らなかったが、これもだいぶ興味深い。機会を見つけてもうすこし調べてみたいと思っている。
最後に、今回の記事は内容の多くを『浮動小数点数小話』に依っている。タイトルに惹かれてなんの気なしに購入したのだが、たいへん面白かった。著者の荒田さん、ありがとうございます。ここで謝意を表して伝わるか分かりませんが、執筆いただいて感謝いたします。なお、この記事に間違いがあった場合は当然ながら全面的に自分の責任です。気軽にご指摘ください。